LeetcodeHard-42接雨水

写在前面：该题转载至leetcode力扣 No.42–接雨水 😃

题目描述：

No.42接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例2：

输入：height = [4,2,0,3,2,5]
输出：9

数据范围：

n == height.length
1 <= n <= 2 * 10⁴
0 <= height[i] <= 10⁵

默认代码模板：

int trap(int* height, int heightSize) {
    
}

题目解析：

该题最容易想到的，也是性能最好的代码，是左右相向双指针。

我们以样例1为例：

下雨前：

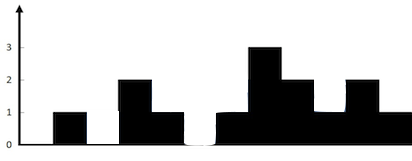
想象l，r两个指针从左右两端向中间行进，我们需要维护左右两个指针，左右两个指针所经过的最大高度以及最后的返回值：

int l=0,r= heightSize-1,sum=0,lMax=0,rMax=0;

在左右指针相遇的时候就已经遍历了全体数组，而一个指针只有在遇到不比他矮的柱子后，他身后经过的空位才能接到雨水，所以只需要对全体数组进行一次遍历，结合遍历过程中指针每一步行进时的反馈，就可以得出全部的接到雨水数，也就是空缺数。

所以我们用一个在左右指针相遇时停止的while循环进行数组遍历：

while(l<r){

}

在每一次遍历中都更新左右指针所经过的最高柱子的高度：

lMax = lMax>height[l]?lMax:height[l];
rMax = rMax>height[r]?rMax:height[r];

 为什么要维护最高柱子高度？

如果指针在记录到经过路径的最高柱子 a 的高度 h 后又遇到了新的不比 a 矮的柱子 b ，那么 a 和 b 之间的所有高度不高于 h 的柱子上方都可以被视为空缺，而 h 与中间的柱子 a_i 的高度 h_i 的高度之差 h-h_i 就是柱子 a_i 上方的空缺所能接的雨水量。

只有在遇到至少不比经过的柱子矮的柱子才能接到雨水，那岂不是在遇到符合条件的柱子前都不知道要不要将遍历到的柱子对应的空缺加入到 sum 里面？所以我们可以选择一个指针行进的条件----前方有不比自己经过的最高柱子矮的柱子时，才会向前行进，即：

if(lMax>rMax){
            sum+=rMax-height[r];
            r--;
        }
        else{
            sum+=lMax-height[l];
            l++;
        }

效果示意：

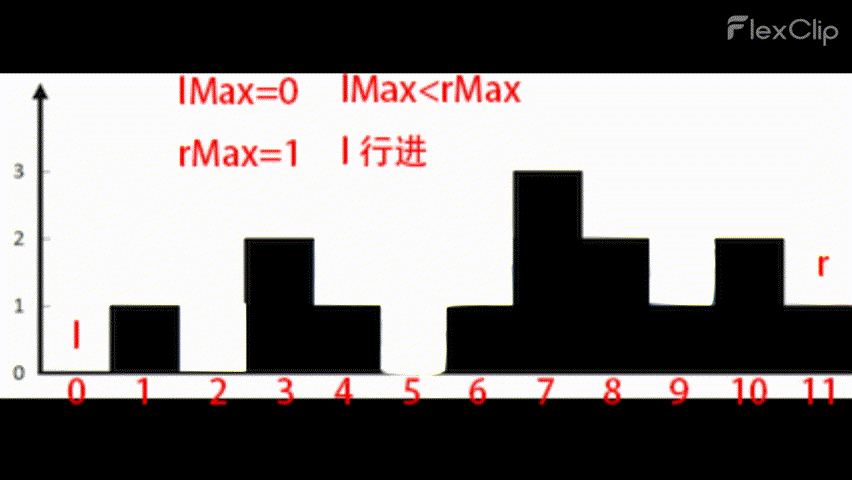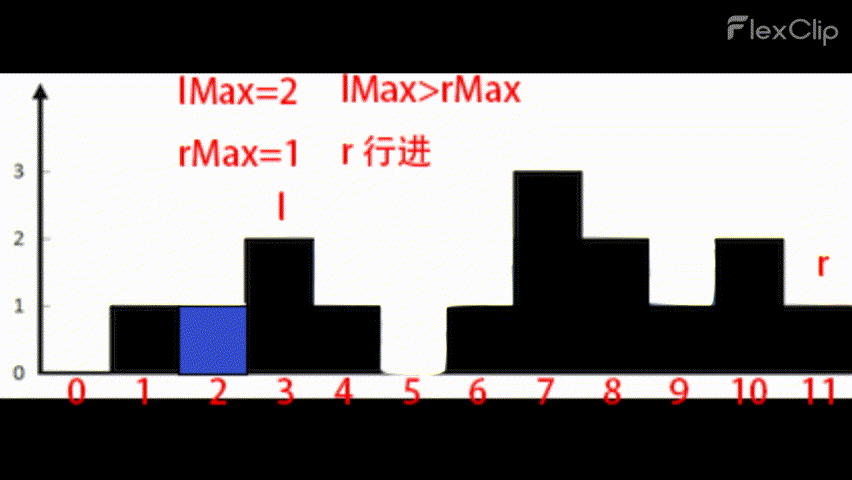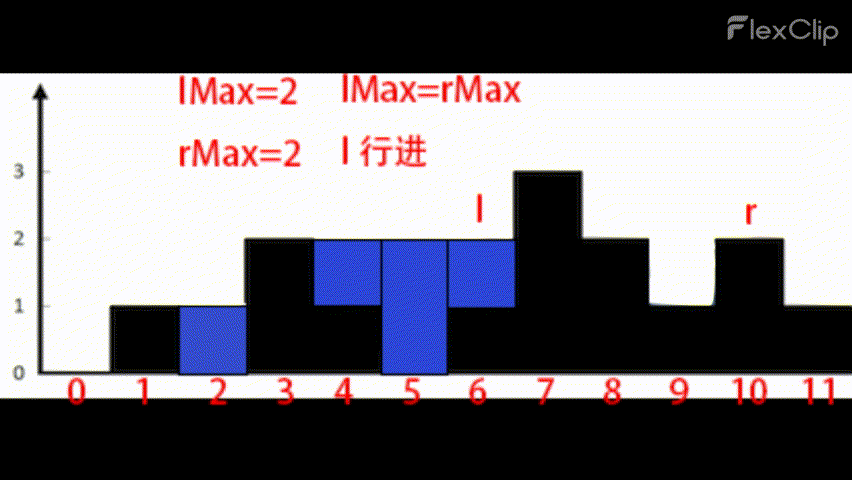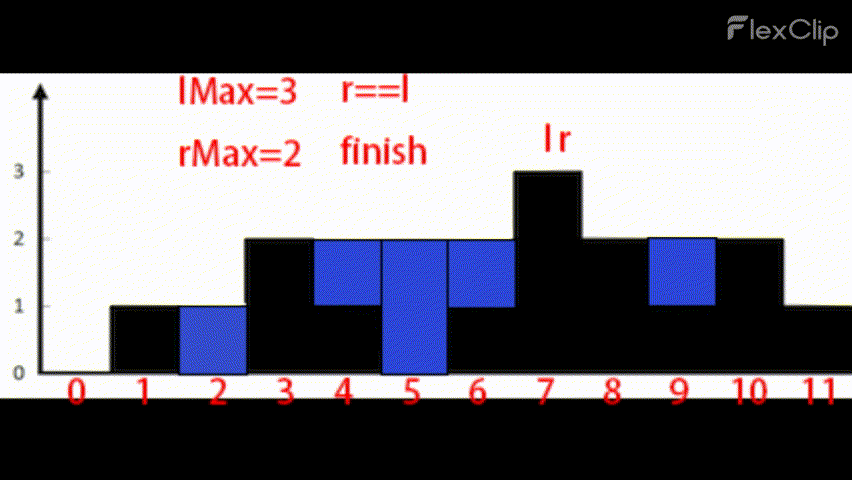
这样，每次循环只移动一个指针行进一步，而这个指针定然会在两个指针顺利会师前遍历到符合条件的新柱子，而在路上遇到的所有矮柱子都会为sum的增长做贡献。

复杂度：

使用双指针求解只需要遍历一次，而且只需要维护常数个变量，所以空间复杂度是O(1),时间复杂度是O(n)。

完整代码：

int trap(int* height, int heightSize) {
    int l=0,r=heightSize-1,sum=0,lMax=0,rMax=0;
    while(l<r){
        lMax = lMax>height[l]?lMax:height[l];
        rMax = rMax>height[r]?rMax:height[r];
        if(lMax>rMax){
            sum+=rMax-height[r];
            r--;
        }
        else{
            sum+=lMax-height[l];
            l++;
        }
    }
    return sum;
}

Connect With Me

TTTTTThank You!